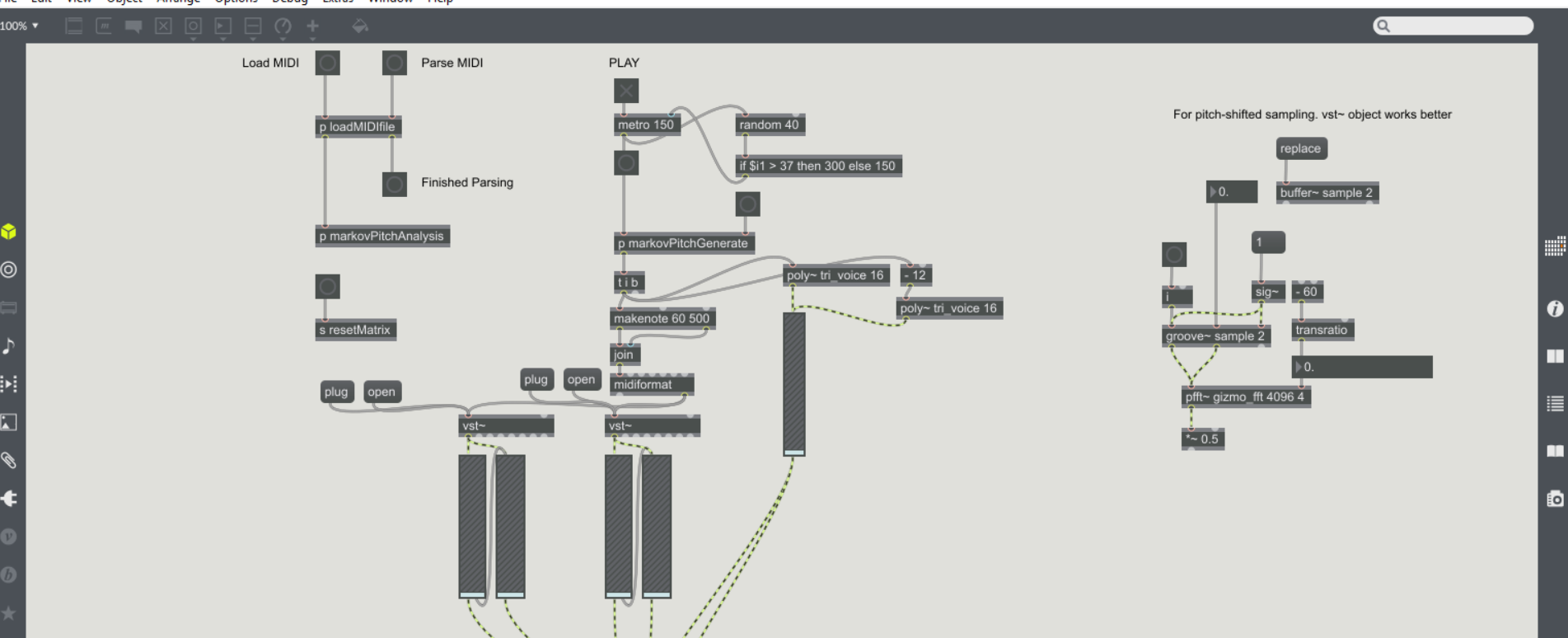
When planning out my first lab day project at Tome, I wanted to create something that bridged the gap between my software engineering position and my musical orchestration passion. An hour or two of research lead me to the idea of using the programming language Max/MSP to write sort of melodic generator. I played with a few generative models like, the cellular automata, Conway’s Game of Life, however I ended up using second order markov chains to achieve a greater sense of melodic consonance
A markov chain, for those unaware, is a stochastic model that describes a sequence of events and the probability of each event occurring based on its precursor(s). Which, in a musical application, means I am analysing an existing musical piece and noting the probability that any given note will play after the note that comes before it (In this case, I’m keeping track of two notes that come before a given note. Hence the ‘second order’ markov chain). With that knowledge, I can generate a whole new melody based on the probabilities. To reach that output, however, a few steps need to be taken.
(Above: The main view of the program when first opened).
The program operates on single track MIDI data which, essentially, is musical notation broken down to a numeric format. For example, the lowest octave of the note ‘C’ is the number 0 and the next highest note, ‘C#’, is the number 1. This numerical sequence continues to the highest value of 127, or the note ‘G’. The MIDI track data is read and parsed into a text file represented as a ‘coll’ (collection) object in Max/MSP. The parsed data reads as a two note sequence followed by the list of all occuring notes that are played after the two note sequencer in the MIDI track. For example, if the MIDI track reads: 1, 15, 17, 1, 15, 19, then the coll object would read: 115, 17 19. Where 115 is the two note sequence and 17 and 19 are the only notes that ever occur after that sequence in the track.
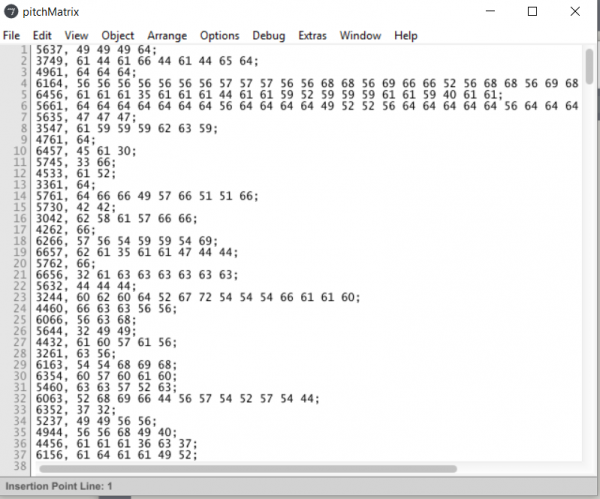
(Above: The parsed MIDI data of the first movement of the ‘Moonlight Sonata’ by Beethoven).
Once we parse a MIDI track, we, essentially, have all the data we need to generate a new melody. However, that does not mean we should stop feeding in MIDI. Because the coll object is never overwritten, we can give the program as many MIDI tracks as necessary. With each influx of data, the program has more notes to work with, more probabilities based on real music, and has “learned” or gotten “smarter” (Keep in mind that the MIDI tracks should all be in the same key musically for a more structured and cohesive sound).
With this data, all we have to do is pick a sequence to start with and use a random number generator to select the next note to play continually selecting new notes based on previously played sequences. This can go on forever, however I elected to allow each note to play only one time for each appearance it has in the collection.
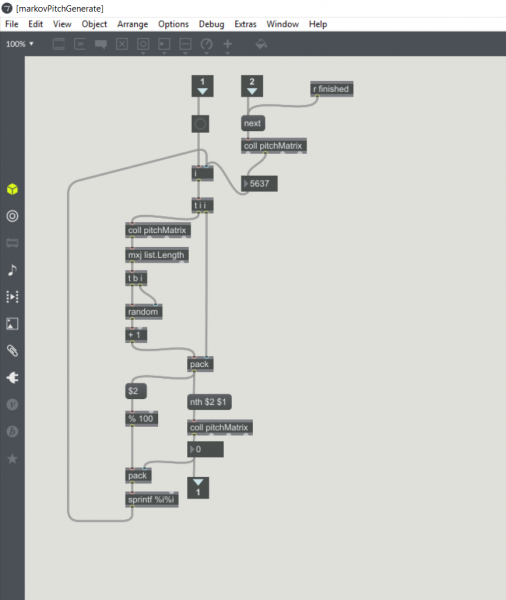
(Above: The algorithm used to generate a weighted random note).
Markov chains are fairly modular, so we could increase the chain’s magnitude to a third order or beyond. Meaning, instead of tracking a 2 note sequence and saving every note the immediately follows it, we’ll track a 3 or a 4 or an X note sequence. The higher magnitude, the greater the likelihood that the new generation will follow the structure of the original pieces and/or pick smarter (more cohesive) note choices based on the probabilities.
I believe this project puts an easy to understand perspective on the links between mathematical probabilistic structures and the abstract concept of artistry. The next steps for a project like this would be to find ways to automate other aspects of music. In this example, we have a melody, but it lacks rhythm, harmony, accompaniment, and so on. A harmonic element is actually fairly simple. Just adding arbitrary numbers to a second MIDI output channel would create harmony no matter how dissonant. The most interesting element, however, is rhythm.
It is certainly probably to devise a second markov chain model that generates rhythm rather than melody. The time between notes would be our tracked element and, again, we’d use probabilities to ascertain how long the program should wait before playing the next note. This dead space in between notes is, generally, what constitutes a valid rhythm. However, I think better rhythm analysis would be based upon pattern matching.
In music theory, there is the term ‘motif’ which describes the smallest part of recognisable, repeatable, music within a larger piece. To lengthen a piece, a composer will often take this motif, be it a melody, a rhythm, or both, and play with it in different ways. Rhythmically, this could mean reversing the motif, speeding it up, slowing it down, playing half of it, etc…This is what I’d like the focus on for rhythm as to add a bit of groundedness to the chaotic melody. I’d like to find the smallest possible (within reason, certainly not a single note) repeated pattern and identify that. If I can identify one, then I don’t need to care about any other rhythmic phrases in the piece. With a rhythmic motif that I could reverse, double, change, or what have you, I could add an extra layer of cohesiveness. The constantly generated melody would be grounded by the repetitious, ever changing, yet familiar rhythm.